El Algoritmo EM y la Bioingeniería Computacional

Autor:

Prof. Paul Cardenas.

Departamento de Bioingeniería

pcardenas@utec.edu.pe

Los datos biológicos son información derivada de organismos vivos y sus productos y a menudo pueden ser muy complejos en comparación con otros tipos de datos. Por ejemplo, los datos biológicos incluyen datos de secuencia, estructura de proteínas, datos genómicos y aminoácidos, sitios de enlaces, y también pueden ser simplemente texto y otros datos secundarios generados por organismos vivos. Debido a su complejidad y abundancia en varias áreas de investigación se requieren modelos probabilísticos pero a menudo los datos biológicos disponibles están incompletos o sin etiquetar para poder entrenar un modelo probabilístico. Casos cotidianos son el diagnóstico médico donde los historiales de los pacientes generalmente incluyen solo resultados de una serie limitada de  examinaciones y no se cuenta con los valores completos de otras examinaciones. Similar al agrupamiento de expresión génica, los datos incompletos surgen debido a que no se conocen las asignaciones del gen a un grupo específico en el modelo probabilístico. 

Considere el siguiente ejemplo juguete (Fig. 1) donde se obtiene el perfil tumoral de pacientes y se requiere segmentarlos. El perfil tumoral se puede usar para ayudar a planificar el tratamiento y predecir si el cáncer regresará o se diseminará a otras partes del cuerpo. La data original (Fig. A) contiene 3 grupos de pacientes con descriptores en 2 dimensiones (X1 y X2). En la mayoría de escenarios, no se conoce a priori las etiquetas de las clases de pertenencia de cada paciente y tampoco el número de grupos dentro de la población (Fig. B). Si usamos el algoritmo EM (expectation-maximization) de forma iterativa es posible identificar los grupos a los que pertenecen los pacientes (Fig. C y D). El modelo generativo converge y es muy parecido a la data original del perfil tumoral  (Fig. A y D). Si se cambia los descriptores a más de 2, se tendrá un problema multidimensional que engloba una aplicación real.  El algoritmo EM se ha usado en problemas de biología computacional relacionados al “dogma central” de la biología molecular, el descubrimiento de motif de secuencia, alineación de secuencias de proteínas, genética de poblaciones, modelos evolutivos y análisis de datos de microarrays de expresión de ARN, etc. A continuación vamos a describir el algoritmo EM y como se usa en problemas reales biológicos.    

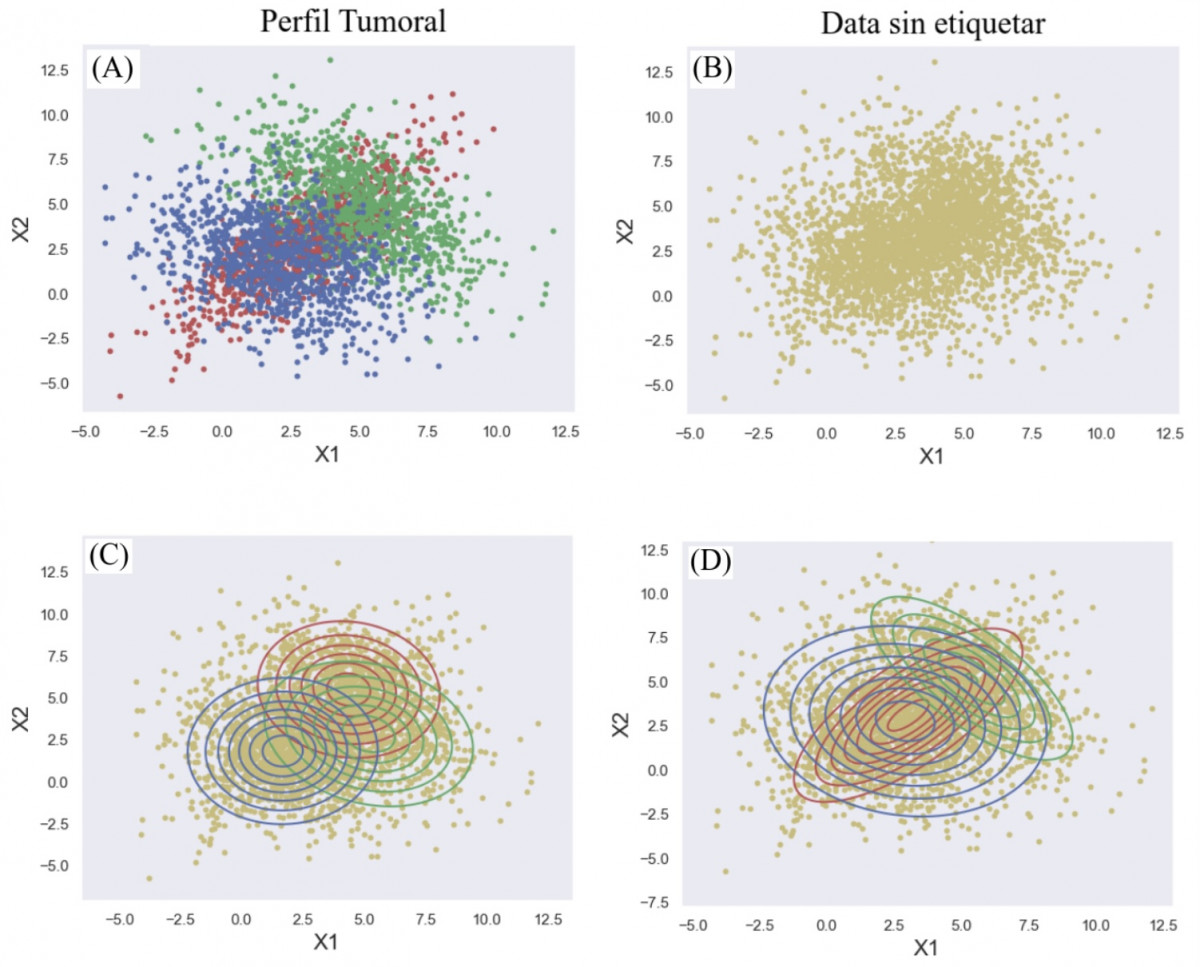
Imagen 1. Segmentación del perfil tumoral de pacientes. Fig. A muestra la data original etiquetada que tiene 3 grupos de pacientes con descriptores en 2 dimensiones (X1 y X2). Fig. B muestra la data original sin etiquetas ya que en la mayoría de escenarios no se conoce a priori las etiquetas de las clases de pertenencia de cada paciente. Segmentación de perfiles tumorales mediante el algoritmo EM (Fig. C: Estado intermedio) y (Fig. D: Estado final). El modelo generativo converge y es muy similar a la data original del perfil tumoral (Fig. A y D).

Fuente. Elaboración propia.

El algoritmo EM permite la estimación de parámetros de modelos probabilísticos con datos incompletos como el ejemplo juguete (Fig. 1). El algoritmo EM fue inicialmente introducido en el contexto de la estimación de la frecuencia génica y fue analizado de manera extensa en el contexto de cadenas ocultas de Markov donde se conoce comúnmente como el método de Baum-Welch. En las últimas dos décadas, la bioingeniería computacional ha pasado de ser una industria artesanal en pañales con un puñado de investigadores a un campo interdisciplinario atractivo, que ha captado la atención y la imaginación de muchos científicos con mentalidad cuantitativa. El algoritmo EM está jugando un rol muy importante durante esta transformación. 

El algoritmo EM es un método iterativo para encontrar estimaciones de maximum likelihood (MLE) o maximum a posteriori (MAP) de parámetros en modelos estadísticos, donde el modelo depende de variables latentes no observadas. El algoritmo EM alterna entre los pasos de aprender una distribución de probabilidad sobre la completación de los datos faltantes dado el modelo actual (conocido como el E-step) y luego volver a estimar los parámetros del modelo utilizando esta completación (conocido como el M-step). En el “E-step” solo se calculan las estadísticas suficientes “esperadas” sobre las completaciones ya que no es necesario obtener la distribución de probabilidad de forma explícita. En el “M-step” se realiza la re-estimación del modelo que se considera como una “maximización” de la probabilidad logarítmica esperada de los datos. 

Los datos observados (X) pueden ser discretos (valores en un set finito o set infinito contable) o continuos (valores en un set infinito incontable) donde cada instancia de los datos puede ser un vector de observaciones. Los valores faltantes o variables latentes (Z) son discretos, extraídos de un número fijo de valores y con una variable latente por data observada. Los parámetros (θ) son valores continuos de dos tipos: los parámetros que están asociados con todos los datos y los asociados con un valor específico de una variable latente. El algoritmo EM en el caso de que θ y Z sean desconocidos es:

1. Se inicializan los parámetros θ a algún valor aleatorio.

2. E-step: Se calcula la probabilidad de cada valor posible de Z, dado θ, (Z|θ)

3. M-step: Luego, se usan los valores recién calculados de Z para calcular una mejor estimación de los parámetros θ.

4. Se repiten los pasos 2 y 3 de forma iterativa hasta llegar a la convergencia de los parámetros.

Este algoritmo se aproxima monótonamente a un mínimo local de la función de costo y es una generalización natural de la estimación de máxima likelihood (MLE) al caso de datos incompletos. En particular, el EM intenta encontrar los parámetros que maximizan la probabilidad logarítmica de los datos observados. La optimización abordada por este algoritmo es más difícil que la optimización usada en MLE.  Esto es debido a que la función objetivo tiene múltiples máximos locales y no tiene solución de forma cerrada para el algoritmo EM en comparación al MLE. El algoritmo EM reduce el problema de optimizar el logaritmo de la probabilidad en una secuencia de subproblemas de optimización más simples, en las cuales las funciones objetivo tienen máximos globales únicos que a menudo se pueden calcular en forma cerrada. 

El algoritmo EM se ha usado para identificar a qué grupo es más probable que pertenezca un gen en particular. Esto es una aplicación muy importante en la expresión génica donde se proporcionan medidas de expresión génica de microarrays para miles de genes en diversas condiciones, y el objetivo es agrupar los vectores de expresión observados en distintos grupos de genes relacionados. Un enfoque es modelar el vector de medidas de expresión para cada gen como una muestra de una distribución gaussiana multivariante asociada con el grupo de ese gen. En este caso, los datos observados (X) corresponden a mediciones de microarrays, los factores latentes no observados (Z) son las asignaciones de genes a grupos, y los parámetros (θ) incluyen las medias y matrices de covarianza de las distribuciones gaussianas multivariadas que representan los patrones de expresión para cada grupo. Para el aprendizaje de parámetros, el algoritmo EM alterna entre calcular probabilidades para las asignaciones de cada gen a cada grupo (E-step) y actualizar las medias y covarianzas del grupo según el conjunto de genes que pertenecen predominantemente a ese grupo (M-step). 

Para encontrar la ubicación más probable de un motif en una secuencia en particular también se usa el algoritmo EM. Esta es otra aplicación que se puede responder en el contexto de búsqueda de motifs donde  se da un set de secuencias de ADN no alineadas y se pide que identifiquen un patrón de longitud W que está presente con variaciones menores en cada secuencia del set. Para aplicar el algoritmo de EM se modela la instancia del motif en cada secuencia con cada letra muestreada de forma IID (independientes e idénticamente distribuidas) de una distribución específica de posición sobre letras, y las letras restantes en cada secuencia como provenientes de una distribución fija. Los datos observados (X) consisten en las letras de las secuencias, los factores latentes no observados (Z) incluyen la posición inicial del motif en cada secuencia y los parámetros (θ) describen las frecuencias (probabilidades) de las letras específicas en la posición para el motif. El algoritmo de EM calcula la distribución de probabilidad sobre las posiciones de inicio del motif para cada secuencia (E-step) y actualiza las frecuencias de las letras del motif en función de los recuentos de las letras esperadas para cada posición en el motif (M-step). 

Otras aplicaciones donde se usa el algoritmo EM son el aprendizaje de dominios de proteínas y familias de ARN, el descubrimiento de módulos transcripcionales, identificación de proteínas, alineación de secuencias de proteínas. El algoritmo EM también se usa ampliamente en la reconstrucción de imágenes médicas, especialmente en tomografía por emisión de positrones, tomografía computarizada por emisión de fotón y tomografía computarizada de rayos X. 

En todas estas aplicaciones, el algoritmo EM proporciona una estrategia simple, fácil de implementar y eficiente para aprender los parámetros de un modelo. Una vez que se conocen estos parámetros, se puede usar la inferencia probabilística para realizar preguntas al modelo proporcionando un mecanismo sencillo para el aprendizaje y construcción de modelos. En general el EM se ha convertido en una herramienta útil para trabajar con datos faltantes y observar variables latentes y proporcionar un mecanismo para construir y entrenar modelos probabilísticos ricos para aplicaciones biológicas. Si estás interesado en aprender más acerca de este y otros algoritmos para resolver problemas reales postula a la carrera de Bioingeniería UTEC.

Bibliografia:

1. Xiaodan, Fan & Yuan, Yuan & Liu, Jun. (2011). Statistical Science 25.

2. Do, C.B. and Batzoglou, S. (2008), Nature Biotechnology, 26, 897

3. Ceppellini, R., Siniscalco, M. & Smith, C.A. Ann. Hum. (1955) Genet. 20, 97. 

4. Hartley, H. Biometrics (1958) 14, 174 . 

5. Baum, L.E., Petrie, T., Soules, G. & Weiss, N. Ann. (1970) Math. Stat. 41, 164. 

6. Dempster, A.P., Laird, N.M. & Rubin, D.B. J. R. (1977) Stat. Soc. Ser. B 39, 1. 

7. Do, C. B., Mahabhashyam, M. S. P., Brudno, M. and Batzoglou, S. (2005). Genome Res. 15 330–340.

8. Weeks, D. E. and Lange, K. (1989). Math. Med. Biol. 6 209–232. 

9. Chen, X. and Blanchette, M. (2007). BMC Bioinformatics.

10. Edlefsen, P. T. (2009). Conditional Baum–Welch, dynamic model surgery, and the three Poisson Dempster–Shafer models.