Docente de UTEC participa en paper publicado en la revista European Journal of Operational Research

Nuestro profesor de la carrera de Ingeniería Industrial, Fabien Cornillier, publicó recientemente un artículo en la destacada revista European Journal of Operational Research, titulado: A recursive time aggregation-disaggregation heuristic for the multidimensional and multi-period precedence-constrained knapsack problem: an application to the open-pit mine block sequencing problem.

Este artículo es un trabajo de investigación desarrollado por el profesor Fabien Cornillier con Pierre Nancel-Pénard del Laboratorio Delphos (Advanced Mining Technology Center, Chile) y Nelson Morales (Civil, Geological and Mining Engineering, Polytechnique Montréal, Cánada) con el objetivo de resolver un problema real de planificación en el sector minero. Es una buena ilustración del potencial de la Investigación de Operaciones en la mejora de la competitividad empresarial.

Se puede descargar el artículo de forma gratuita hasta el 16 de junio de 2022 en la editorial Elsevier en estas direcciones: https://bit.ly/3MtteTQ (versión web) y https://bit.ly/3Ls1T3f (PDF). 

A continuación, Fabien Cornillier nos cuenta más sobre este logro:

Cuéntanos un poco de tu publicación, ¿qué problema resuelve en la industria minera? 

Esta publicación trata de un problema importante y difícil de la industria minera a tajo abierto. En minas a tajo abierto, representamos el subsuelo como un conjunto de grandes bloques paralelepipédicos. La explotación de la mina consiste en extraer esos bloques del subsuelo para generar una utilidad. Sin embargo, los bloques no se pueden extraer de manera arbitraria. Si observamos una mina a tajo abierto, nos damos cuenta que tiene una forma de cono invertido para garantizar la estabilidad de las paredes, ello implica que para extraer un bloque es necesario primero extraer los bloques que se encuentren arriba de este (ver Figura 1). También, todos los bloques no son iguales: unos generan utilidades positivas, otros cuestan más de extraer que el valor de los minerales que contienen, generando así pérdidas.

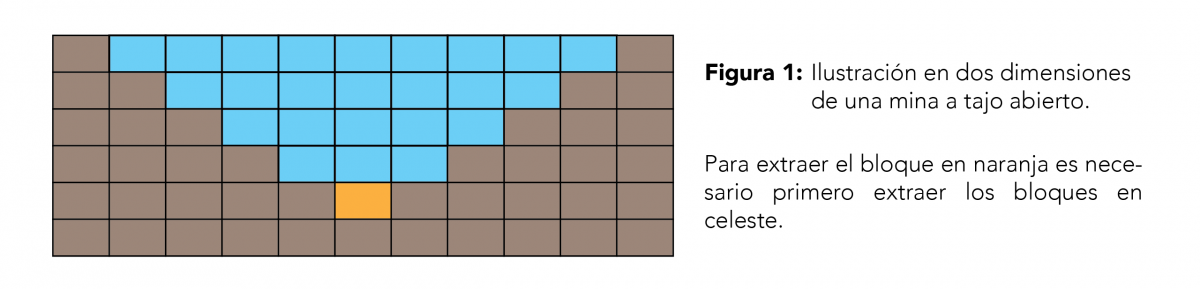
Como para todas las empresas, el objetivo de la minera es maximizar su utilidad, la cual depende de cómo elegimos los bloques por extraer, cuándo y en qué orden extraerlos. Esos problemas de optimización son extremadamente difíciles de resolver, aún más en minas grandes que pueden contener millones de bloques. 

En este contexto ya difícil, una consideración práctica viene a complicar el problema: tenemos que garantizar que las soluciones encontradas permiten alimentar sin discontinuidad las plantas que procesan los bloques, lo que exige tener siempre, y durante años, bloques con un mínimo de minerales listos para alimentarlas. Este requerimiento vuelve el problema tan difícil que en muchos casos ningún método conocido de optimización suele ser capaz de encontrar soluciones. 

Con mis colegas Pierre Nancel-Pénard y Nelson Morales, proponemos un método que permite encontrar muy buenas soluciones en problemas de planificación extremadamente grandes con más de 2 millones de bloques, 40 millones de variables y 700 millones de restricciones, cuando los otros métodos no encuentran ninguna solución. 

¿Cómo este problema puede influenciar la competitividad de una mina? 

Aparte de factores externos tales como los precios de los minerales en los mercados internacionales de materias primas sobre los cuales la empresa minera no tiene ningún control, la utilidad de una mina depende de la manera de explotarla a lo largo de su vida que puede ir hasta 30 o 40 años para las minas más grandes. Su utilidad depende de la eficiencia de la explotación, es decir de su planificación que consiste esencialmente en responder a las preguntas: ¿Qué bloques extraer? Y ¿Cuándo?. En el transcurso de la explotación de un yacimiento, la planificación de la extracción de bloques  explica en gran parte los resultados financieros generados. Las herramientas de optimización son también esenciales al momento de decidir de invertir o no en la explotación de un nuevo yacimiento. Naturalmente, los inversionistas están más dispuestos a financiar la explotación de un nuevo yacimiento si la minera es capaz de demostrar su rentabilidad futura, cuando la diferencia entre un yacimiento rentable y otro que no lo es radica en gran medida en la optimización de la planificación. 

¿Cuál fue la innovación en el artículo publicado? 

Los métodos clásicos descomponen la vida útil de la mina en periodos, meses o años. Si por ejemplo queremos explotar un yacimiento durante 20 periodos, nos interesa saber qué bloques se deberían extraer cada periodo. De hecho, es literalmente imposible resolver grandes problemas de 20 periodos de una sola vez. Resolver un problema con 2 periodos es mucho más fácil, eso lo sabemos hacer. Así, para reducir la dificultad de un problema grande, lo podemos dividir en una serie de subproblemas de 2 periodos esperando que la combinación de sus soluciones permita obtener una buena solución para los 20 periodos. 

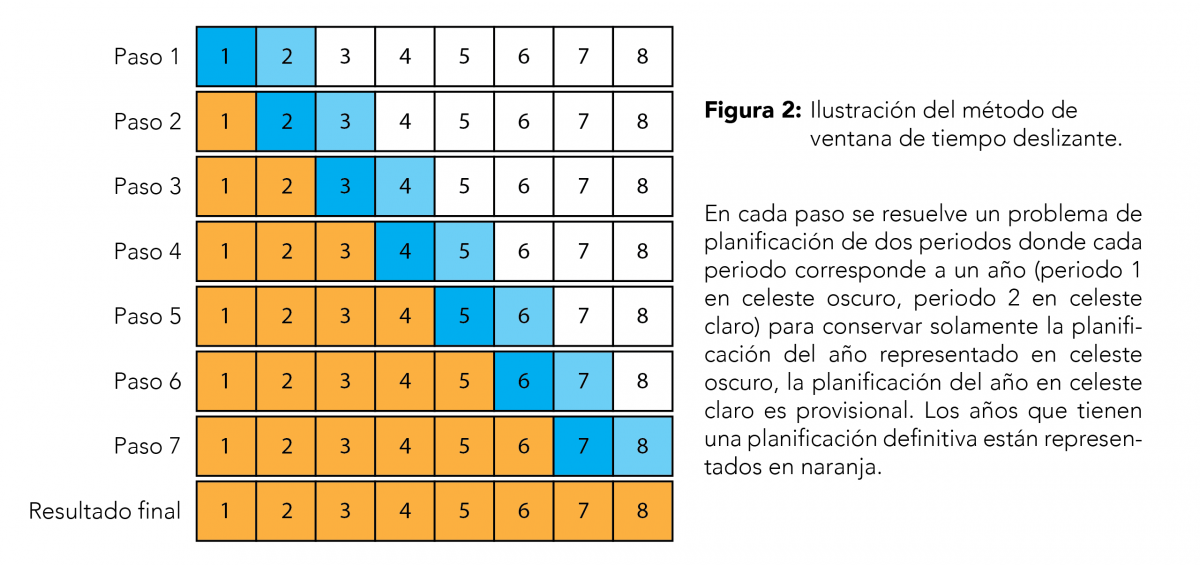
En problemas multiperiodos se utiliza generalmente una técnica clásica conocida como ventana de tiempo deslizante. Por ejemplo, podemos proceder de la manera siguiente: resolvemos un subproblema que considera solamente los períodos 1 y 2 para obtener la planificación del periodos 1, luego resolvemos un subproblema que considera solamente los períodos 2 y 3 para obtener la planificación del periodos 2, y así sucesivamente hasta obtener una planificación completa para todos los periodos (ver ejemplo con 8 años en la Figura 2). Esa técnica puede funcionar muy bien. Lamentablemente, es demasiado miope: se planifica cada vez un año tomando en cuenta la información de sólo un año en adelante. En ciertas circunstancias, necesitamos tener una visión más global para realizar que las mejores decisiones a corto plazo pueden perjudicar los resultados a largo plazo. Este es el caso de la minería dónde buscamos un plan de actividad que garantice el funcionamiento continuo de las plantas de procesamiento. El método de ventana de tiempo deslizante genera una excelente planificación en los primeros años a costa de imposibilidades en los años posteriores.

En el artículo, proponemos un método de agregación-desagregación, una forma muy distinta de descomponer el problema. Por ejemplo, para obtener una planificación de 8 años, agregamos los años de tal manera de obtener un problema con 2 periodos donde el primer periodo corresponde a los 4 primeros años, y el segundo periodo a los 4 últimos años (ver Figura 3). Así, sabemos qué bloques extraer en los primeros 4 años y que bloques extraer en los 4 últimos. A continuación, utilizamos la misma técnica para determinar si un bloque extraído en los primeros 4 años se debe extraer en los primeros 2 años (años 1 y 2) o en los 2 años siguientes (años 3 y 4). Igual para determinar si un bloque extraído en los últimos 4 años se debe extraer en los años 5 y 6 o en los años 7 y 8. Procedemos así sucesivamente hasta saber exactamente en qué año extraer cada bloque.

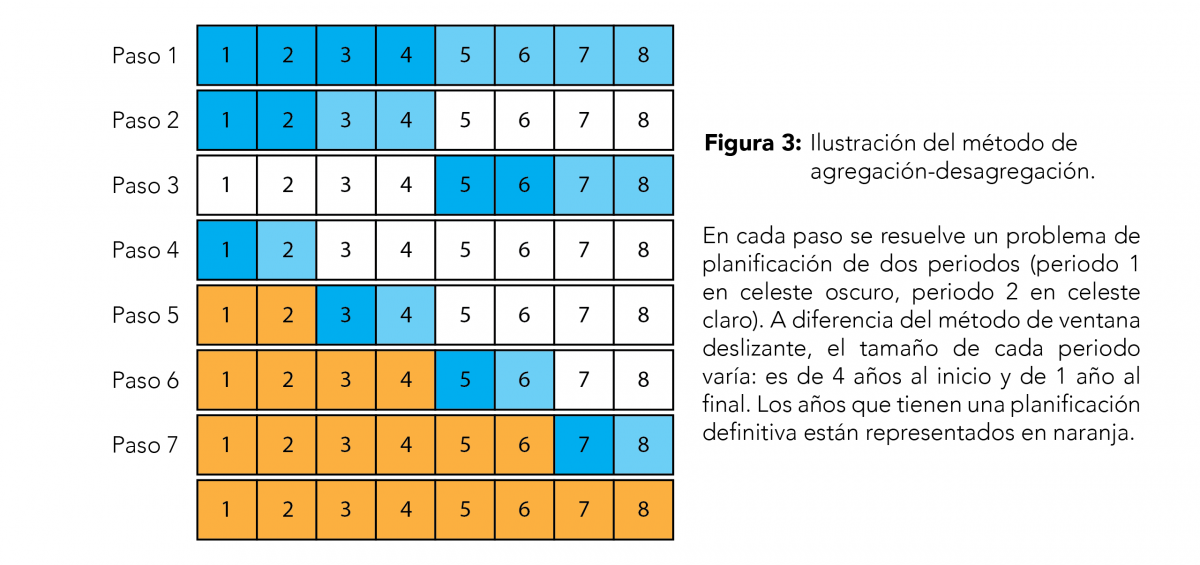
Con este método el problema se resuelve a diferentes escalas, con diferentes resoluciones: una resolución de 4 años por periodo al inicio, luego de 2 años, y en fin de 1 año. El hecho es que esta técnica permite una visión completa del horizonte de tiempo desde el primer paso, no tiene la miopía tan problemática de los métodos de ventana de tiempo deslizante, los resultados obtenidos lo demuestran.

¿Podría aplicarse el mismo método fuera del contexto de una mina con alguna adaptación? 

Varios problemas multiperiodos  de planificación tienen características similares al problema de planificación minera y podrían beneficiarse de ese nuevo método. Podría ser el único método apropiado en ciertas circunstancias, en particular cuando las decisiones de corto plazo tienen un impacto determinante sobre los resultados a largo plazo. Podemos tomar el ejemplo de un proyecto en el cual es deseable obtener un flujo de caja positivo todos los años, es decir no tener nunca un año con pérdidas. En término de aplicaciones, podemos pensar en la planificación de la ampliación de redes de telecomunicaciones o de distribución de gas por ejemplo. 

¿En qué otros proyectos mineros estás trabajando o te gustaría trabajar? 

Además de la minería a tajo abierto que hasta ahora concentra la mayor parte de los esfuerzos de investigación en planificación minera, la minería subterránea, que es el futuro de la minería, tiene muchos retos interesantes y poco estudiados. Otro tema de interés es la dimensión ecológica de la planificación minera. La minería tiene un impacto ambiental muy importante, cualquier mejora, incluso la más pequeña, puede tener un impacto tangible sobre las condiciones de vida de las poblaciones locales y, más generalmente, sobre el estado de nuestro planeta. Todavía es un punto ciego de la investigación. 

En tu opinión, ¿qué habilidades consideras básicas para ser un profesional en Investigación Operativa? 

La primera etapa en la resolución de un problema es reconocer que este existe en verdad para identificarlo. Se necesita curiosidad intelectual, pensamiento crítico. Además es necesario tener la habilidad de conectar ideas. El pensamiento asociativo es una dimensión importante de la creatividad. En la investigación operativa, estas habilidades tendrían un valor limitado si no se combinarán con la expertise. No se puede detectar e identificar una oportunidad de aplicación de métodos de optimización sin tener un buen conocimiento de los problemas clásicos de optimización conjugado a una cierta experiencia propia o ajena, por ejemplo por la lectura de artículos científicos o profesionales. 

Luego de identificar un problema de interés, empieza la fase de profundización que consiste en intercambiar con todas las partes involucradas para llegar a una comprensión aguda del problema y su contexto. Esa fase es esencial y no necesariamente la más simple ni la más corta del proceso. Necesita paciencia, habilidades de comunicación y de escucha activa. 

Una vez los detalles del problema aclarados, empieza la fase de modelamiento y de resolución que implica separar los factores más importantes que tomaremos en consideración de los factores no esenciales que podremos eliminar para construir una representación matemática o lógica del problema. Desde esa fase, es esencial tener un buen conocimiento de los diversos métodos de resolución con sus límites respectivos. La construcción del modelo es un ir y venir entre tres mundos: el mundo real, el modelo y los métodos de resolución. Se necesitan habilidades analíticas, importantes aptitudes para la resolución de problemas y una cierta experiencia de modelamiento y optimización.